11・引力と向心力と角速度
引力の角速度と向心力の角速度
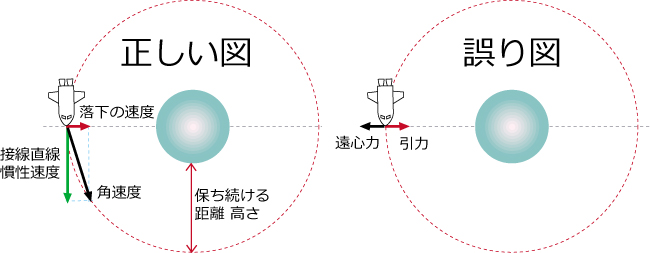
1・つり合った天体の周回の力
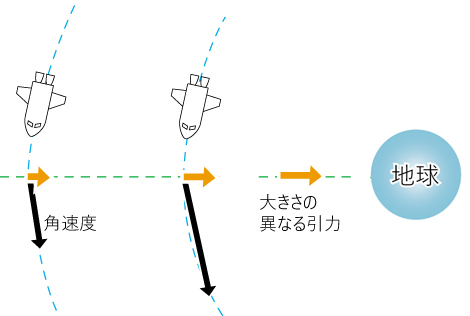
・引力は天体に近づくほど大きくなります。
・接線直線慣性速度は衛星となる以前から持っていたものです。
これが引力と合体して 角速度という加速度になるので
つり合うことができます。
2・衛星が曲がって進むための力
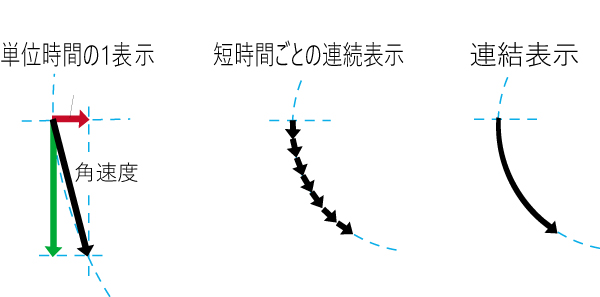
大きくカーブして進むのが周回や回転の運動です。
これら運動は角速度で定義されています。
聞き慣れない言葉ですが、この際 覚えましょう。
3・つながる物体の回転の力
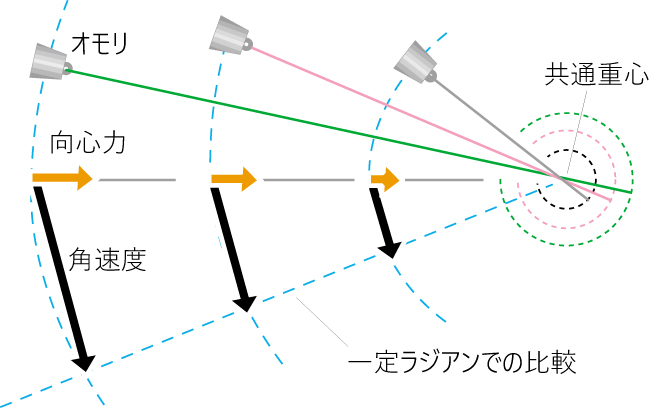
・向心力は半径距離が短くなるほど小さくなります。
つり合いの引力とは逆で、大きく異なりますす。
・重りを引くための手先の回転が右端の円です。
大きい半径であれば回す手先の仕事量が増えて、
向心力も接線速度も大きくなります。
小さい半径ほど小い力で周回が可能になります。
・角速度は弧度法を使っており[ラジアン/秒]が単位ですが、
このホームページで使っている意味は、
『曲がって進む速度の定義ができる』
『宇宙での周回運動の定義に最適』
周回の原動力として認識していただくために使っています。
最適の定義と言葉が既にあるのですから 利用しましょう。
・接線直線慣性速度の動きは、引力や向心力によって内側に曲げ
られてしまうので円周の外に出ることはありません。
法線外向きに作用する慣性力ではありません。
遠心力の代わと思わないように、、冒頭の図の説明です。
・天体の公転や、向心力で何かが回ると、同じ運動が限りなく
繰り返されます。これを慣性の運動としてしまうのは早計で
す、慣性ではありません、方向が変わり続けるので加速度運
動です。
4・置きバケツの回転の力
<「09」の追記の設問の図です>
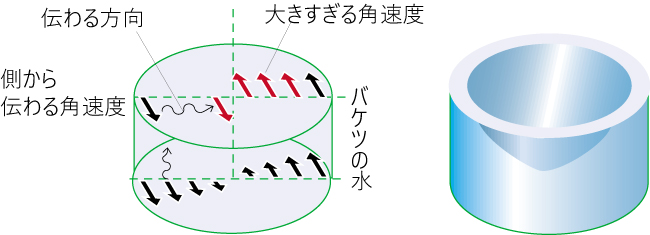
ターンテーブルの上で回るバケツの水です。
バケツの側と底から内へと角速度が伝わっていきます。
底の水はバケツの底から伝わるため正常値に近い。
上部は側から大きい角速度を そのまま内へ伝えます。
強すぎる接線速度を向心力が引き込められないために、
そこの水は接線速度の方向へ動かされてしまいます。
5・
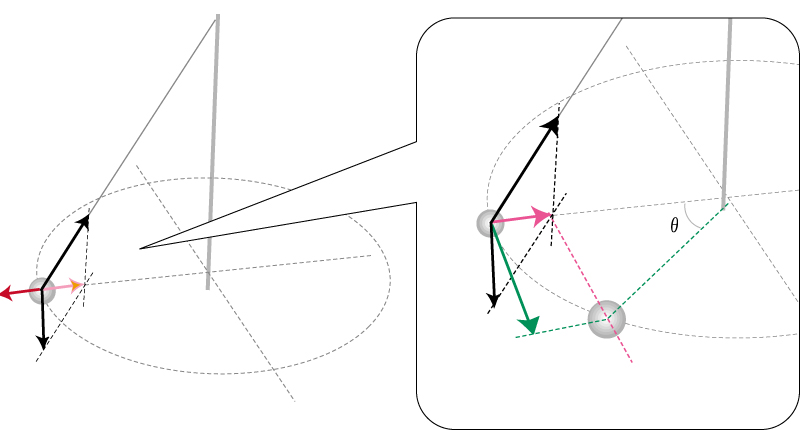
回る振り子の円運動の説明に見られる図に少し手を加えて
みました。オモリが半径を保って周回するのを、向心力と
遠心力で説明することが多いのですが、遠心力を止めて、
接線速度(緑の矢印)で説明すれば良いのでは…。
弧度法について
角速度について
等速円運動について
「先生による説明」の動画です
2020.12.7
11→→
HPへ
→→
スマホへ