17・潮汐の発生原因を探す

　〔前半〕 遠心力の真偽
　〔後半〕 潮汐と月の位置

　 天体角速度と 解決したのか潮汐


取り付きやすい話から、結論から…　上空で強力な大型砲を使い水平に弾丸を発射すれば、猛スピードで長い長い距離を飛んでいきます。

ところが地球の引力で自然に落下（自由落下）してしまいます、でも地球の地面は球体で丸いため、落ちても落ちても地面に届きません。

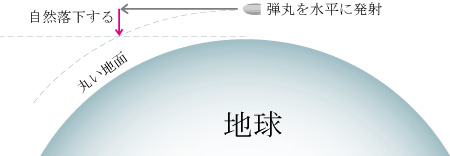
弾丸が空洞で中にアリさんが居たなら、高速で進みながらも自由落下するため弾丸は無重力の状態になり、中のアリさんも浮かんでいます。

次に月や地球など宇宙の関係を調べてみます。

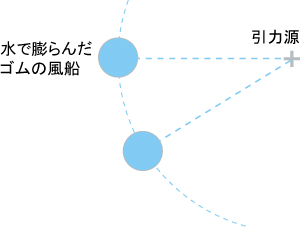
引力源の位置に地球があり、Ａの位置に月がいて、月が地球を周回しています。月が地球との距離を保っている（つり合っている）状態を図にすれば下図のようなことになるでしょう。

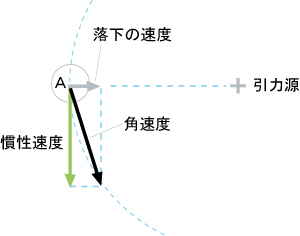
月は接線方向に慣性速度を持った状態で地球に自由な落下を続けます。両作用は合力されて黒矢印になります。

黒矢印の角度変更は絶え間なく続いていますので それぞれの矢印は非常に短い（長く表示できない）のですがが、時間を伸ばして分かり易く表示します。

今の月にとって、緑矢印、青矢印、黒矢印は、３つ同時に存在しているのではなく、合力された黒矢印だけが存在することになります。

連続して方向を内側に変更する円運動をしている黒矢印には角速度と言われる名前が付けられています。

引力源とＡを逆に見ても同様の角速度だけの運動が成り立っており、両者は引き合う作用が存在しない関係となり つり合います。質量が大差であれば重い方の円運動は極々小さくなります。

どなたもご存知のことで、これで説明すべて完了。
のハズです…


いっぽうで引力と遠心力が対抗することで月は地球との距離を保っている（つり合っている）とする理論があります。

下図のＡ位置で、左向きの遠心力（赤矢印）と右向きの引力が等価であれば月は左右どちらにも移動せずつり合うとしています。

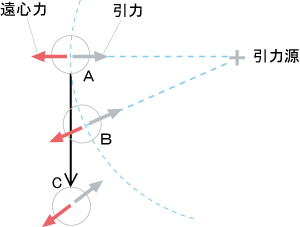
その後月はＢの位置に来るのですが、引力が中心に向かうのは良しとして、　遠心力の赤矢印の方向が変化するのはなぜでしょうか？Ｂ位置の赤矢印の方向を変えた力はどこにあるのでしょう？

最も重要なことは、Ａ位置でつり合っている月は、そのときに持っている速度の方向を変えることができません。なぜなら働き続ける引力に対応して相分の遠心力で差し引きゼロにしていますから。

よって月はＡ位置で保持していた接線方向であるＣの方向に移動してしまうことになります。赤矢印と灰矢印が一直線のセットで方向を変えると（ゆずって）想定しても、どの方向を向いても力は差し引きゼロです。

慣性の等速直線運動というのはありますが、慣性の等速円(周回)運動というのは存在しないと思いますが…正円を周回すれば等速円運動ですが方向が逐次変わる力が加わっているので慣性ではありませんね。回転する剛体の慣性モーメントとは異なるような、、

まずは、遠心力として上図の赤矢印を想定するのは誤りだとわかります。（現実は灰色矢印も存在しません）


つぎに 紐で結んだ石の代わりに水を満たしたゴムの球体で、引力が働かない場合の遠心力を考えてみます。バネとオモリでも同じです。

下図の円運動は（中心が仮に不動として）中心に引力源が存在せず紐で引っ張っています。ゴム球は卵形に変形します、洗濯機の脱水槽でなら平たくつぶれるでしょう。これはつり合う遠心力が存在するようにみえますが…

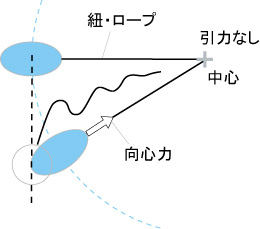
こんな説明でどうでしょうか…

ゴム球が真横にあるとき、中心で紐をゆるめてやる。すると持ち前の慣性速度で黒点線の接線方向に進み、自由になったゴム球は真球に戻ります。

中心において素早く紐を手繰り寄せて円運動の半径まで戻します。するとゴム球が中心に向かう「円運動の特徴である向心力」の作用が見えます。

向心力に引張られることで ゴム球は 静止慣性の抵抗と相まって卵形に変形します。

慣性には直線移動慣性と静止慣性の２種しかありませんが、ゴム球は、接線方向へは、直線移動慣性を有し、同時に、それの直角方向には静止慣性も備わっています。非引力円運動は同時に２種の慣性が実働している運動ですね。

「紐をゆるめる、円運動の半径まで引張る」、この作業を限りなく短く速くすれば、静止慣性に対して向心力が働き続けることになり、ゴム球は「静止慣性抵抗により変形」した状態で円運動をすることとなります。

ここでは 静止慣性の抵抗による変形させる力を「慣性力」と特定して進めさせてください。

結局ゴム球には、接線方向の慣性速度が一定なので新しい力は 向心力だけが作用していることになります。

慣性力の扱い…
向心力に抵抗する慣性力は外向きの力ではありません、向心力に引きずられる荷物のようなものです、法線の外方向へ引っ張る力ではありません。

外向き体感は…
向心力は、円運動ゆえに方向が変わり続けるため常に新しい力 になります。この新しい向心力には 新しい慣性力が発生し続けます。これが見落とされて…『外向きの力が別途に発生している』の、思い違いになっているようです。

人が円運動に参加して、人の接線移動を向心力で円周まで曲げ続けられると、反対向きの慣性抵抗を感じ続けます。その際、回転中心との距離が変化していないので慣性抵抗を意識できず、法線外向きの別途の力だ、反作用だ、つまり遠心力だ、と思い違いします。

反作用と遠心力…
『体感者には外向きの力と感じるので それを遠心力として処理してもよい』は 正しくありません。人は反作用を思いますが、それは出現しない力です。『２階から飛び降りて骨折したので地面の反作用は恐ろしい』みたいなことです。

遠心力の不合理…
『遠心力』＝『-向心力』と設定して、数式表示などしていますが、円運動に『-向心力』が存在すれば向心力と差し引きでゼロになり 円運動ができません。

回転座標系内に居る観測者に円運動は見えないのだから「話は合っている」ように思えますが、それでは遠心力の発生原因が存在しません。


つり合った 引力 の作用による場合は状況が違うように思います。
　　　
引力はゴム球がいくら大きくとも中の水を含め全位置に（原子レベルの細かさで）くまなく働きます。よってすべての場所に角速度を働かせることができます。

向心力であれば、紐からゴム球へと伝わり、伝わった場所で慣性力が発生して変形します。引力ではすべての場所で位置に応じた大きさで同時発生の慣性力となりますから変形はしないでしょう。

観測者が何処にあっても慣性力を感じたり変形を見つけることが出来ません、よって「無し」となります。ゴム球は真球で周回するでしょう。

ただし、位置に応じた大きさの角速度ですから、引力源に近い場所と遠い場所とで大小が生じます。これは、対象の天体が 流体で かつ 引力源に 近い という条件付きで、変形か流動を伴うでしょう。

また、紐とゴム球の円運動に働くのは向心力ひとつだけですから、天体の円運動も引力による引き合う力が唯一存在している として正しいように思えます。　しかし、円運動する両者の引き合う力は、周回する運動（角速度の方向変換）に全て消費されており２番目の図に戻ります。

引力は存在するが、つり合う天体同士の間に引き合う作用は存在しない状況が作られています。重力(引力)場の中に重力(引力)の消滅する空間・次元が出現することは、ブラックホールなどと異なり、現実的でたいへん面白い現象だと思います。静止衛星は良い実例です。

宇宙の恒星や惑星や星間物質や銀河までも含めすべてが、引き合う作用の消滅した空間・次元であればこそ存在できています。言い換えますとすべては相当に速いスピードで動き回っていることになります。短い人類の文明では数億年以上もある銀河の周回運動を知ることができません。

もし、つり合うのではなく引力源に真っ直ぐ 衝突に至る落下（衝突落下）をしているのなら、角速度は存在しません、引力は落下の内側でより大きく、外側で小さく働くことになりゴム球は変形するでしょう。

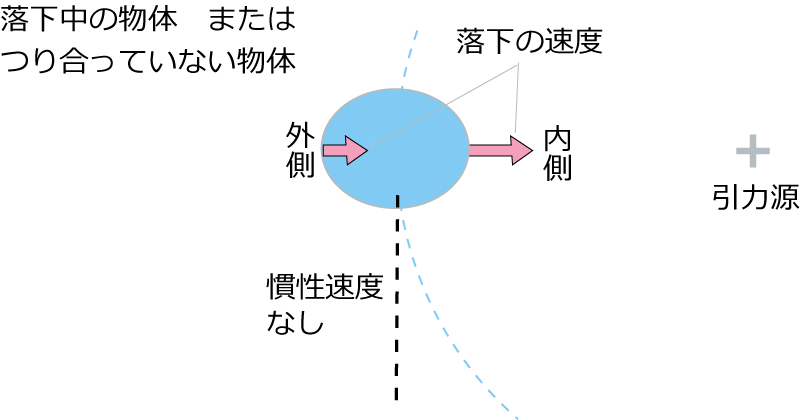
さらにゴム球が角速度を持って旋回しながら衝突落下しているのなら、変形は程度問題ということでしょう。

※周回は慣性速度と自由落下速度の合力とするのであれば、自由落下速度は内で大きく 外で小さいのだから、変形に至るのでは？と思えますが…

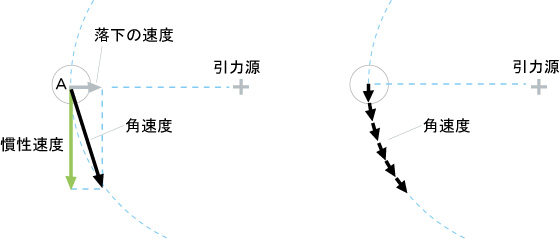
２番目の図を正確に表現すれば、極々短い角速度矢印があるだけです、慣性速度と自由落下速度は瞬時に角速度に生まれ変わります。２番目の図は便宜の拡長であって変形を言えるための時間はないのです。

また、自由落下は継続しても速度は加速されません、微細な方向変更を伴っていますので、都度 元の大きさの 新しい自由落下となっています。

まとめると…

非引力円運動では…
Ａ１ ・慣性力が組み込まれている円運動
　　〈慣性力はよく見える〉 …紐とゴム球、バネと重り
　　　　　　　　　　　　　　 遠心分離器
　　〈慣性力は確認しにくい〉…コマ、車輪、プロペラ

Ａ２ ・慣性力が組み込まれていない準円運動
　　〈慣性力は部分的確認となる〉…脱水機

引力円運動では…
Ｂ１ ・つり合っているなら慣性力は存在しない
　　〈ひとつの角速度を確認する〉…剛体天体、衛星
Ｂ２ ・上に同じ
　　〈複数の角速度が確認できる〉…潮汐、銀河の腕

Ａ Ｂ、１　２ は仕組みが異なる別の運動です。


引力やその慣性力は所在や有無も正しく説明されているでしょう。にもかかわらず、紐とゴム球にも存在しない遠心力を、仕組みの異なる引力円運動にまで持ち込んでしまった。結果、ゴチャ混ぜの運動になり、慣性力のみならずつり合いまでが誤解されることになってしまったのでは…

≪連携する天体には引力作用による変形が生じている≫と、紐・ゴム球と同じ変形が天体にも起きている…や、つり合いとは異なる 衝突に至る落下の運動をもって潮汐の原因とする≫…などと混同や誤解をしないようにしたいと思います。

ネットの潮汐説明にはたくさんの誤りがあるのでは…

１、紐と引力を同じと考えて区別していないこと
２、地球と月は変形しないこと
３、月とのつり合いの遠心力は存在しないこと
４、裏の満潮に働く慣性力（遠心力）も存在しないこと
５、表の満潮は月の引力が引張っているのではないこと
６、得た結果の不都合を誤差のせいだとする更なる誤り
　　…多くは、満潮時刻に月が最高の位置には居なくて
　　　　6時間前後遅れるとする説明もしていません。

　
潮汐と月の位置

満潮が諸々の理由で月の南中に遅れる
…この理論は本当なのでしょうか…

月と潮汐の見方について一言…　図‐1 は北極の上から見ています。地球の自転は左回りしますので、満潮が月の最高位置に比べて遅れている図なのですが、、、　地表に居る我々には、地面は静止して、太陽、月、満潮、すべてが右に回って見えます。 それは理科で学ぶ、「静止地面と天球の図」回転座標系の図です。

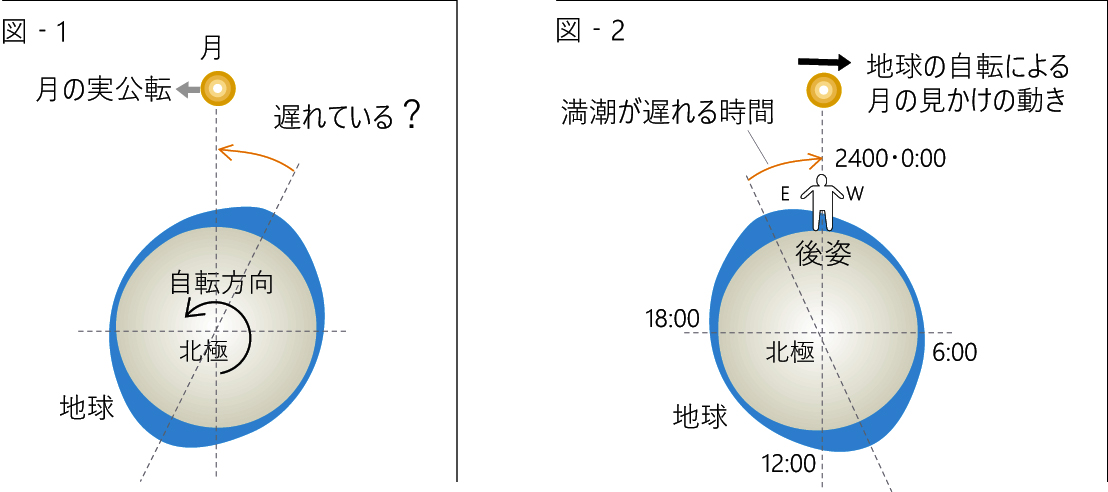
図‐２がそれで、日本から月を見上げると体は南を向きます(図の人物は後ろ向き)、右手は西を、左手は東を示します。　時間は左(E)が未来で 右(W)が過去になります。その人物から見て、月に遅れる満潮は図‐２となります。これらを承知されたうえで お進みください。

誤差で遅れると言いますが…海岸で見る満潮の水位は月が真上に昇る前に東から西へ過ぎていきます。

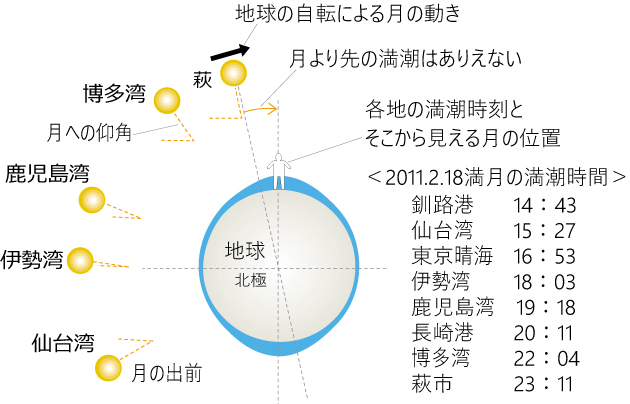
満潮が 月より左にあれば遅れで、右にあれば早すぎ、となります。満月は真夜中の０時に南中しますから、伊勢では 24-18：03＝約6時間早すぎ となり、遅れる理論に反し 図のような現実になります(図を90度右に回し 月を真上にして図２と比較)。

閉鎖的海域ゆえ遅れがある日本海や瀬戸内海の満潮でさえ月の東仰角40〜80度あたりで満潮のほうが先に通り過ぎていきます。東京や仙台など北部では月が出る前に過ぎていきます。ぜひお近くの海岸でご検証ください！

遅れるのであれば、月の東仰角が90度以上、つまり最上位置を過ぎて後に満潮となるはずですが、そうなってはいません。その意味するところは…

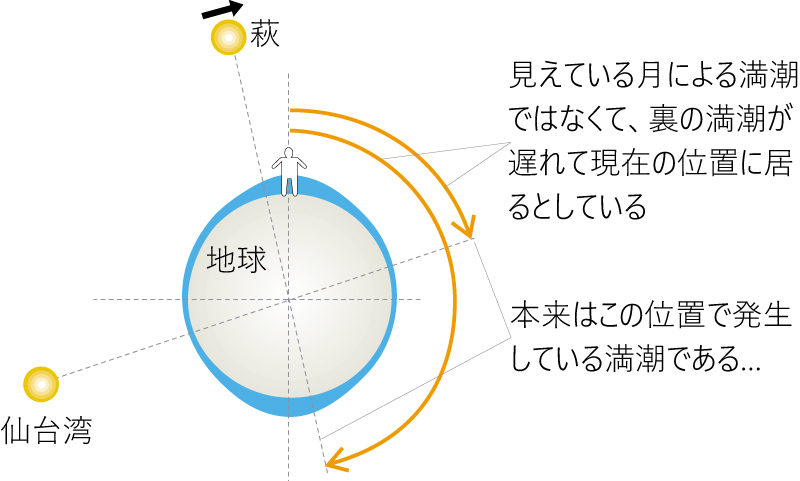
萩市を例にしますと、裏の満潮の遅れは誤差による6時間（約90度）に加え仰角で約75度遅れるとします、合計165度あまり、11時間遅れている、と言うのですが

6時間ずれたり遅れたりの差は、反対の出来事が生じる意味合いとなります、11時間もの差であれば次の満潮の直前となります。…誰が見ても変です、それゆえ誰もここには触れようとはしないのでしょう。

さらに言えば…引張られるのであれば、地球がどんなに速く自転しても海水は月に一番近い場所が盛り上がります。地形にも多少影響されるでしょうが、まず前や後ろに大きくずれることはありません。どなたも経験的にご存知のことです。

満潮の時刻に月が最上位置(南中)にないのですから、引張られてはいないとういことです。

引張るのであれば誤差を設けること自体が誤りでしょう、遅れるとする誤差の在り方にもまったくの無理があります。

…潮汐の問題は何一つ解決していません、そっくり残ったままです…

　　　２０１３．６．１７　

17→→ ＨＰへ 　→→ スマホへ