18・引力作用が角速度に変身＜角速度は天体が公転する原動力＞

小さな公転の角速度が潮汐を招く

1・引力の引き合い作用
　

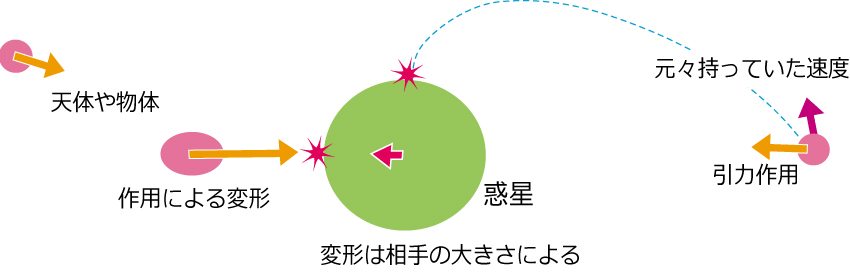
引力の引き合いが作用しているときの天体とは… 互いに接近しつつあるときや、太陽や惑星に物体が衝突している場合に見られます。作用は、互いの天体の距離が近いほど大きく、離れるほど小さくなります。

2・つり合う天体の出現

　
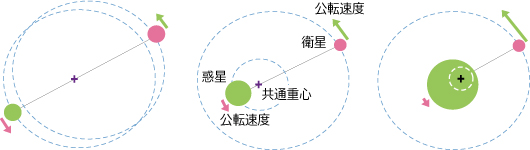
惑星と衛星のような「つり合い」が生まれると、それら親子天体は接近や衝突をしなくなります。親子の周回は楕円やほぼ円形の公転運動となります。円運動をする速度は角速度と呼ばれ、相手天体を公転させます(上図の赤と緑の矢印)。

3・天体が公転する力は何処にあるのか

惑星と衛星は自分の質量に見合った引力を相手に及ぼします。これは言い換えると、相手の直線慣性速度(慣性)を内に引っ張ることで 合体して角速度(加速度＝力)に生まれ変わることです。

　　
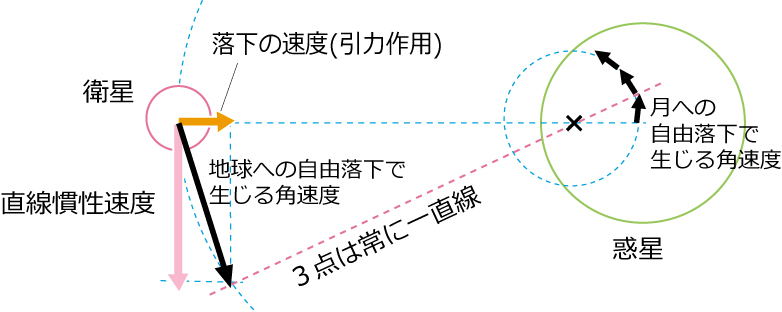
角速度は絶え間なく方向を変えるために、ごく短い矢印が連続する動きとなります。図では長時間の表示をして分かりやすくしています。角速度は天体が公転するための唯一無二の「力」です

4・月の引力も地球に小さな公転をさせている

　　

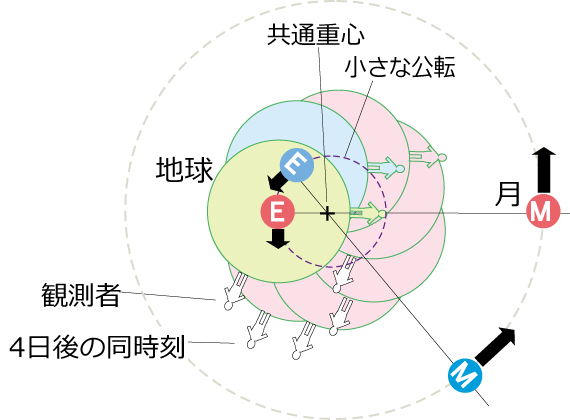
月が公転すれば、地球にも つり合うための角速度が生まれます(３の図ひっくり返し)。Ｅ、共通重心、Ｍ、の三点は常に一直線で周回しています。地球の自転を一時無しとしても、人物（読者でも同じ）から見て共通重心は27日かけて地球内部を一周しています。

5・距離差の引力大小は角速度に生きている

　　　　

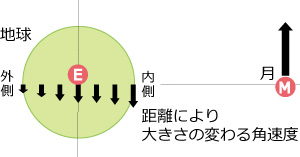
月が地球に与えている、位置に応じた角速度の違いは、力で遥かに勝る地球の引力が作っている硬さが無理やり隠してしまい、地上では識別できなくなります。

ところが、硬くない流体の海があったので作用の大小が内側と外側で姿を現しました。「20→地球の潮汐」に続きます。

６・潮汐などの解明が思わしくないのは…

地球や月が周回する運動について、よく言われているモデルというのがあって、「微小固形物ガス」が一体となって太陽を回っていて、それが引力集積して現在の惑星に成長した…だから惑星の公転は、浮遊物時代の運動を引き継いでいる。

また 衛星の公転は、浮遊物の局所周回があって、それを引き継いでいる。こちらは 随分と以前にNASAが発表しています。

天体の周回は、曲がって進んで元の位置に戻ることの繰り返しだから慣性運動だろう、と いうことではありませんね…

「曲がって進む」の時点で加速度（力）であることがわかります。どんなに微細な浮遊物であっても、自然に周回なぞしません、慣性の周回なぞありません。

また、中学や高校で「見かけの力」であり 存在しない力です、と学ぶ遠心力は、どこかで 回れ右して 頻繁に使用する安易さです。そのせいで遠心力を言わない正しい解析方法から逸脱しているようです。いくつかの例が「9」の追記にあります。

さらに、月の及ぼす引力が地球の 月側と反対側とで大小する説がありますが、これは月と地球がつり合うのではなくて、衝突に至る接近中であるときの姿です、最初の１図に戻ります。


　　　２０１１．１．１８　(2020.11.25リメイク)

18→→ ＨＰへ 　→→ スマホへ